

The incenter is the intersection of the angle bisectors of each of the 3 interior angles of any given triangle. The incenter is also the center of the circle that is inscribed within a circle. In fact, this circle is the largest circle that can be constructed within a circle that is tangent to all sides of the triangle.
Click Here for a construction of the incenter in GSP.
Proof:
For the incenter, each line created is the angle bisector of each of triangle ABC's angles. Thus, we can construct the angle bisectors of C and B. Because the angle bisectors are not parallel, they will meet at a point, which we will call O.
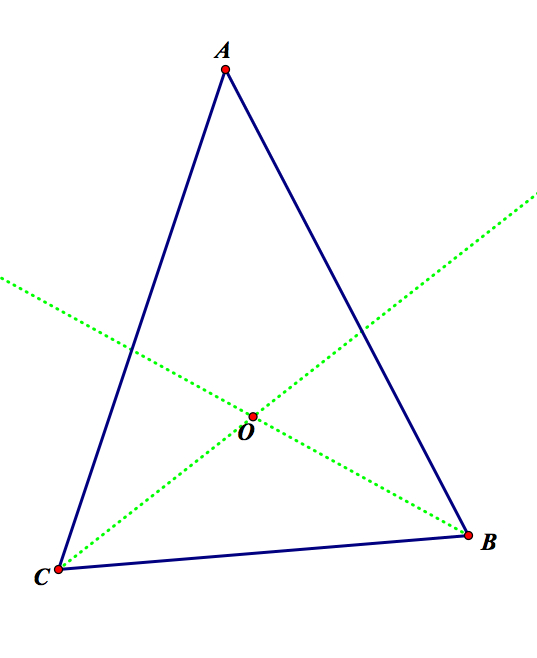
Now, constructing perpendicular lines from point O creates a line segment from O to E, on segment AC, F, on segment CB, and G, on segment AB.
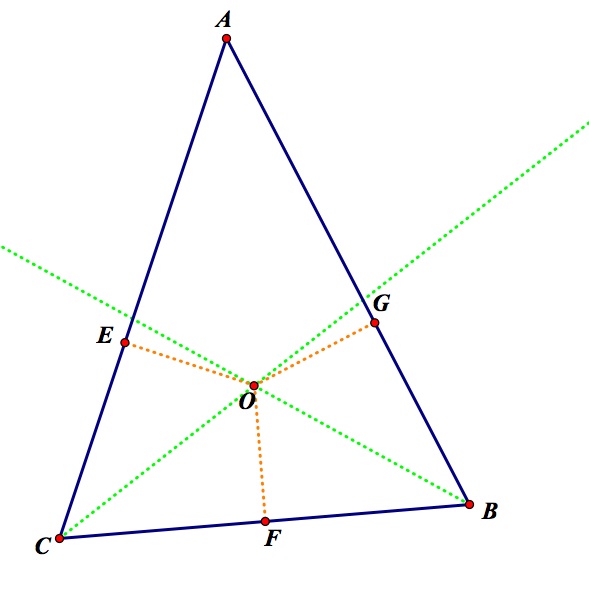
From this we can show that triangle EOC is congruent to triangle FOC. This is true by the angle – side – angle triangle theorem. This is due to the fact that angle ECO and FCO are congruent because their made by the angle bisector through O. Therefore, segments EO and FO are congruent.
Similarly, triangle FOB is congruent to triangle GOB by the angle –side- angle theorem. Therefore, segment FO and GO are congruent. From this and transitivity we can state that FO = GO= EO.
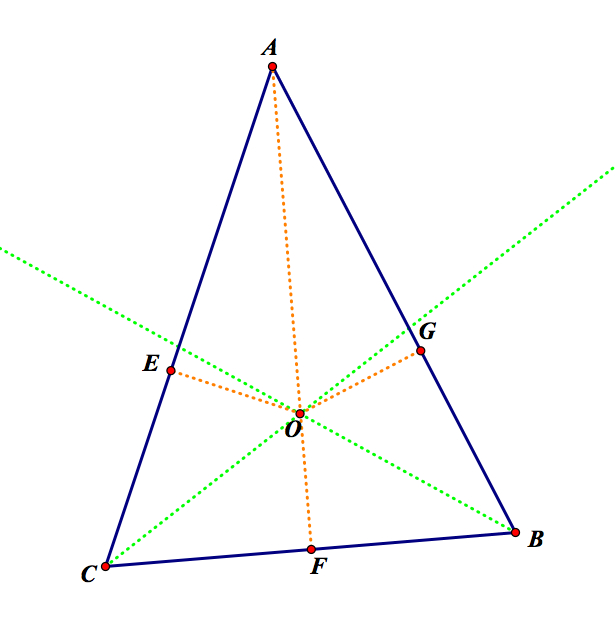
Now, constructing the line from A to O provides a line and creates two more triangles. Triangle AOE is a right angle because the segment OE is perpendicular to AC. Furthermore, the triangle AOG is also a right triangle because OG is a perpendicular segment to AB. Since both are right triangles and each shares the segment AO, which is the hypotenuse of both triangles. Since angle EAO and angle GAO and both have a right angle, it follows that angles AOE and AOG by the triangle sum theorem. Thus, by angle-side-angle these triangles are congruent. The segment AO is the angle bisector and it intersects the other angle bisectors at O.
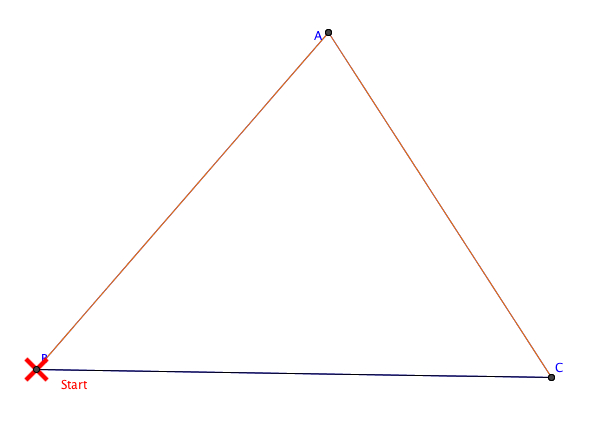
Here's the scenario:
.jpg) |
Barney is in the triangular room shown here. He walks from a point on BC parallel to AC. When he reaches AB, he turns and walks parallel to BC. When he reaches AC, he turns and walks parallel to AB. Try moving the starting point in Geogebra! |
When Barney starts the vertex B or the vertex C, it follows that Barney will actually be traveling along the sides of the triangle.
 |
 |
Thus, the distance traveled by Barney is simply the perimeter of the triangle.
When Barney starts at the midpoint of BC, it follows that the Barney will travel about the medial triangle. Take a look!

Not only does Barney start at the midpoint of BC, but he also hits each wall at their midpoints. The distance traveled by Barney if he travels along the medial triangle is half of the distance traveled when he starts at one of the vertices. This is because the medial triangle is composed of the points that are the midpoint of the original triangle. Thus, the smaller triangle is 1/2 of the larger one.
Check out this Geogebra construction.
Now, if Barney starts anywhere along the segment BC, Barney will still find his way back to the starting point.
.jpg)
The question is: What is the distance traveled by Barney when an arbitrary point is chosen along the segment BC. Using geogebra, we can use the distance feature to determine the total distance traveled. Varying this point, we can determine whether the distance changes or remains constant for all points other than the vertex or midpoint.
Form using the distance features in geogebra, it is evident that the distance traveled is equal to the total distance (perimeter) of the triangle ABC. Thus, regardless if Barney chooses to travel around the outer perimeter of triangle ABC or take the route stated in this problem, he will be traveling the same distance.
Return to Incenter Exploration